Category: Tools

Bin Diameter (feet)
Angle of Repose (degrees)	Grain Depth at Wall (feet)
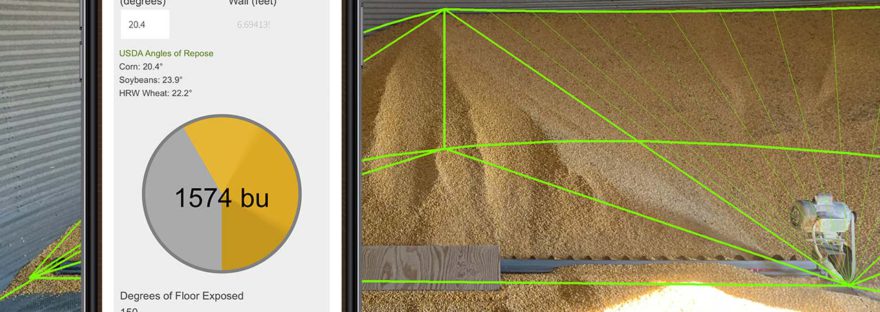
USDA Angles of Repose Corn: 20.4° Soybeans: 23.9° HRW Wheat: 22.2°
Adjust for Test Weight
Market Test Weight	Actual Test Weight
Corn: 56 Soybeans: 60 Wheat: 60
error
Degrees of Floor Exposed 45

Method of Calculation

These calculations require 3 inputs as you see above

• Diameter of Bin
• Angle of Repose OR Depth of Grain at the wall (both are needed eventually, so inputing one will calculate the other)
• Degrees of floor exposed

Initial Geometry

During the initial stage of emptying a bin with a sweep auger, the pile of grain can be approximated in 3 geometric shapes

• (Part of) An inverted cone
• Two tetrahedrons
• Two circle segments (cut diagonally in half) to fill in the curved wall shape behind the tetrahedrons

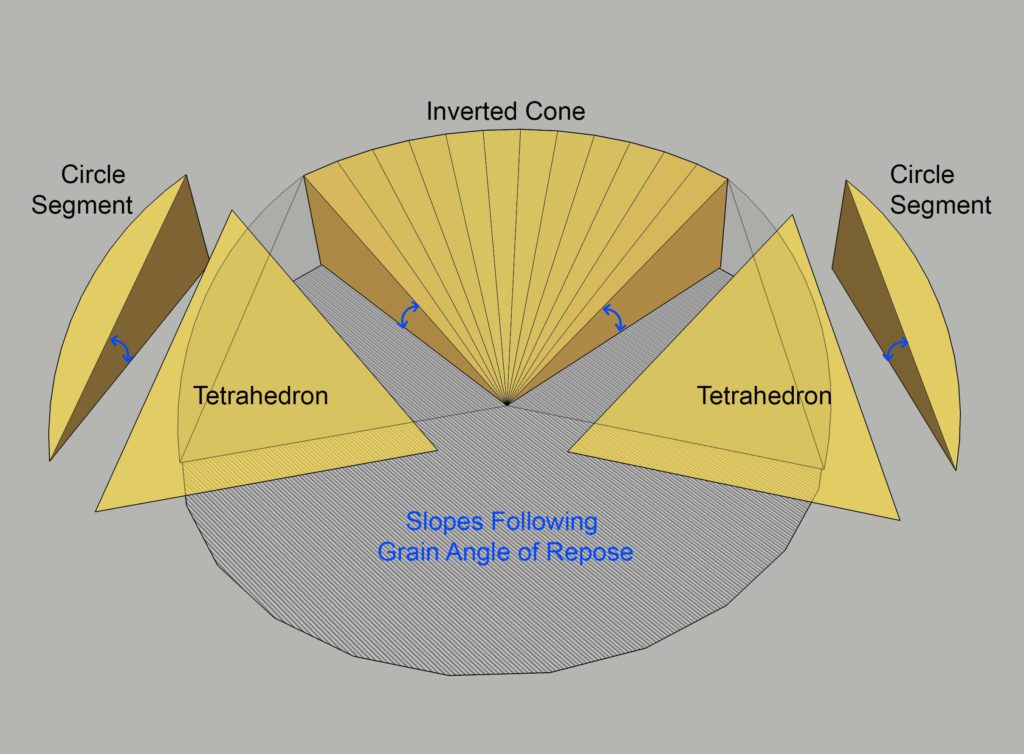
Inverted Cone

The inverted cone is simple to calculate. First, calculate the volume of a cylinder the diameter of the bin and as tall as the height of the grain at the wall. Then, calculate the volume of a cone with the same footprint and height and subtract that cone of air from the cylinder of grain. Since the volume of a cone which you're subtracting is 1/3 the base surface area times the height, a shortcut for an inverted cone is to just take 2/3 of the volume of the starting cylinder.

The volume for the entire inverted cone would represent a bin which has quit running out of the center sump and has never had a side sump open. We'll need to only use a percent of this based on how many degrees of the floor are exposed and how many are taken up by the tetrahedrons.

originalConeVolume = (π * binRadius^2)*(grainDepthAtWall)*(2/3)

percentOfConeRemaining = (360 - (floorExposedDegrees + (tetrahedronAngle*2))) / 360

remainingConeVolume = originalConeVolume * percentOfConeRemaining

Tetrahedrons

We already know that the two sides of the tetrahedron not facing the wall will have to be the radius of the bin. I also think it's reasonable to make the wall side the radius of the bin (and thus, an equilateral triangle base) because:

• That's roughly what it looks like standing in front of it
• This makes the angle of repose from the top point of the tetrahedron to the outside of the sweep equal to that from the top point to the center sump
• This simplifies the calculations because the tetrahedron bases will always be 60°

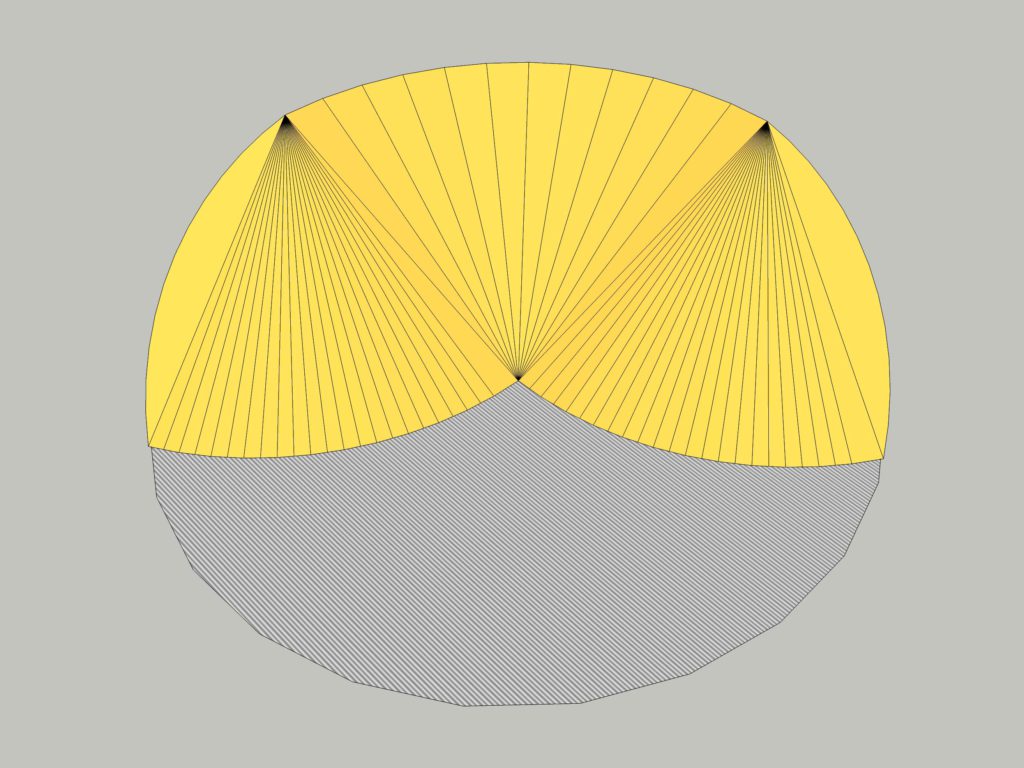
In a perfect world, the grain should fan out from the peak at its angle of repose as visualized above. But in practice, it's constrained by a flat sweep auger on one end and on the other end you may have side sumps that have created a flat edge by the time the sweep is started. Plus, you'll be running the sweep deeper into the center of the pile with less contact on the ends, so it's averaging somewhere in the middle. So I think the flat tetrahedrons with an equilateral base are a reasonable representation.

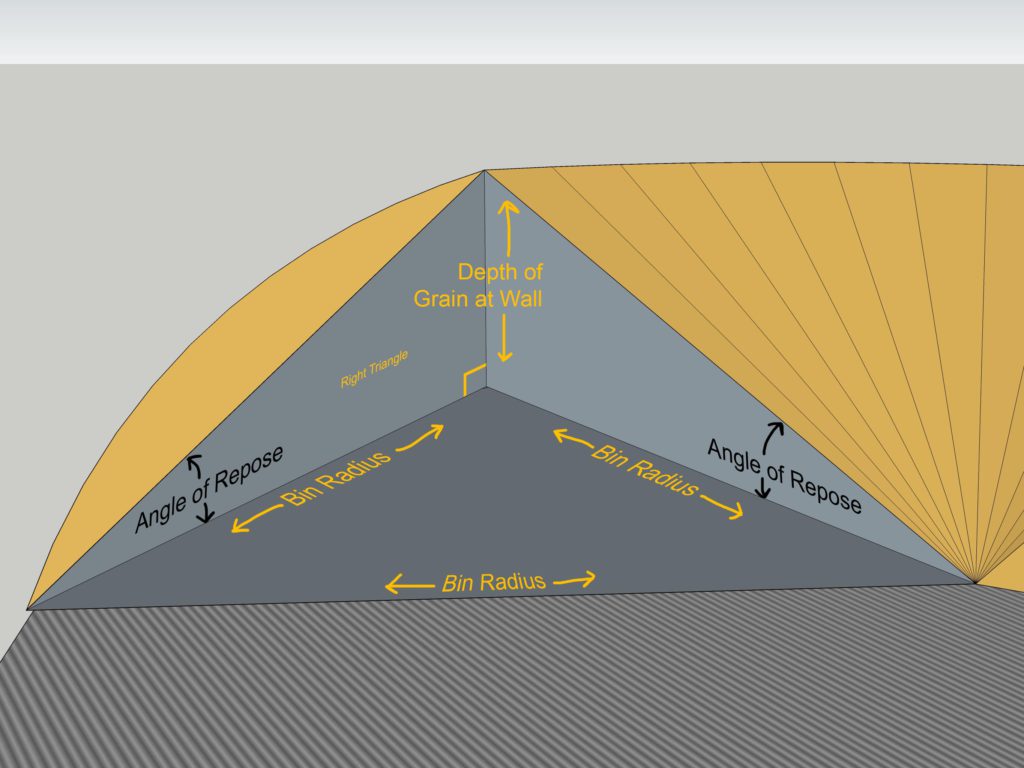
To calculate the volume of the tetrahedron, we can take the surface area of the base times 1/3 of the height. Heron's formula can be used to get the surface area of a triangle with 3 known sides.

semiP = (binRadius * 3) / 2

tetBaseArea = sqrt( semiP * (semiP-binRadius) * (semiP-binRadius) * (semiP-binRadius) )

Then, multiply that by the depth of the grain at the wall, and divide by 3.

tetrahedronVolume = tetBaseArea * grainDepthAtWall / 3

Circle Segments

Finally, we need to account for the sliver between the flat-backed tetrahedron and the curved bin wall. This is called a segment of a circle and is straightforward to calculate given that the angle will always be 60° for an equilateral triangle base.

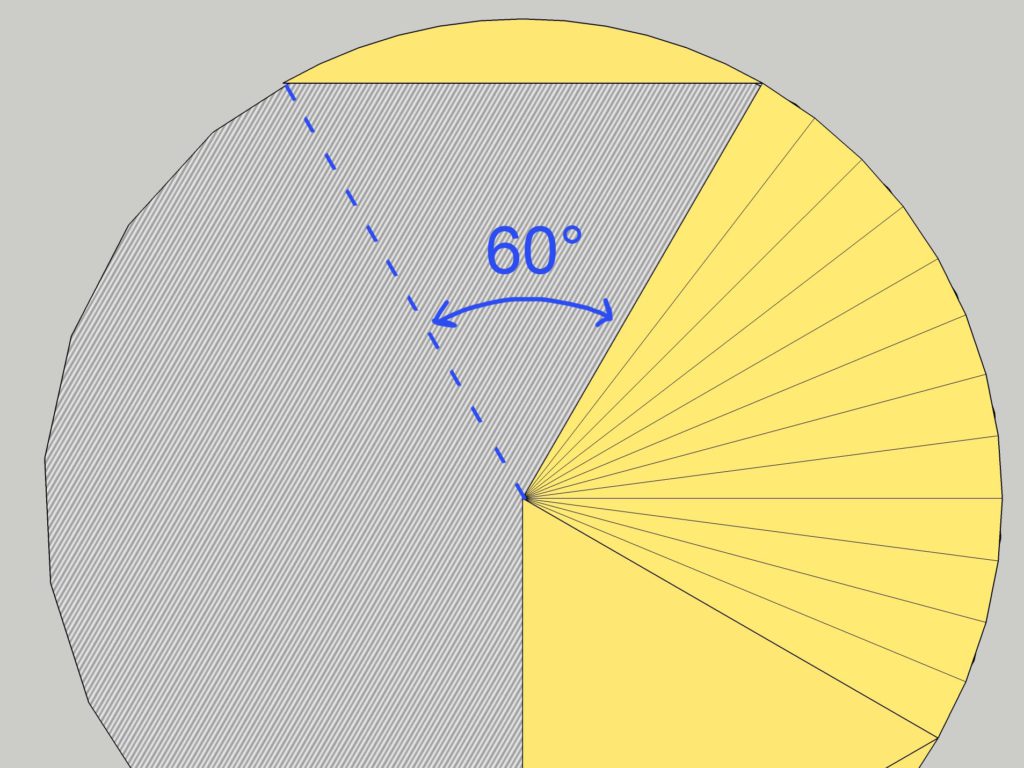
The formula for the area of a segment is:

((tetBaseAngle * π) / 360) - (sin(tetBaseAngle) / 2)) * binRadius^2

Since it will always be 60° in this method, we can compute out all the angle stuff into one coefficient to multiply by binRadius^2.

0.181172147412159 * binRadius^2

Now that we have the surface area of the base, we can get the volume by multiplying it by the depth of the grain at the wall and dividing by 2. (I don't have a math expert on the internet telling me this is the formula for a diagonally cut extruded segment, but generally if you cut a shape in half along a symmetrical line, it's simply base * height / 2.)

Now simply add together the inverted cone and two of the identical tetrahedrons and circle segments, and you have total cubic footage. Then divide by 1.24446 cubic feet per bushel.

Ending Geometry

When finishing a bin, the original inverted cone eventually goes away and you start eating down a single symmetrical pile of two (shrinking) tetrahedrons and segments behind them. Given that we established the original tetrahedrons above at 60° each, this transition occurs when 240° of the floor is exposed (with 120° of grain remaining). From this point forward, the tetrahedrons get narrower (less than 60°) and the grain height at the wall gets shorter.

Tetrahedrons

First we'll need to calculate the width of the side of the tetrahedron facing the wall. We know the two other sides (bin radius) and the angle connecting them (half of the remaining pile angle) so we can use the cosine rule to get the length opposing the angle.

wallSideLength = sqrt(sideA^2 + sideB^2 - 2 * sideA * sideB * cos(halfRemainingGrainAngle))

Now that the width of the wall side is known, we can calculate the depth of the pile at the peak in conjunction with the angle of repose. This triangle on the wall side is a right triangle, so the sohcahtoa rules apply and the tangent function would be used.

With some rearranging of the equation, the formula would be:

pilePeakDepth = tan(angleOfRepose) * wallSideLength

Calculating the volume would work the same as before; use Heron's formula with two bin radii and the wall side length calculated a bit ago, then multiply by the pile peak depth and divide by 3.

Circle Segments

These work the same as earlier, except we can't take any 60° shortcuts.

((tetBaseAngle * π) / 360) - (sin(tetBaseAngle) / 2)) * binRadius^2

The wall depth is known from above, so that would be multiplied by this footprint surface area and divided by two.

Put together two of these tetrahedrons and two circle segments, divide by 1.24446 cubic feet per bushel, and you're set.

Accuracy

SketchUp

I created the 3D models in SketchUp not only to help visualize the geometry, but because I can check the volume of each 3D polygon. I found and corrected two calculation errors through checking it this way.

Initial Geometry

This was with 150° of clean floor on a 36' bin with a 20.4° angle of repose- the same as shown in the models photos above. Numbers are in cubic feet.

	SketchUp	Calculator
Inverted Cone	1,133	1,130
Tetrahedron	313	313
Circle Segment	104	98
Total	1,967 ft3	1,952 ft3

In this case the calculator is showing 15 ft³ (12 bushels) less than the SketchUp model. This is within 1% and variance can be explained by SketchUp trying to make rounded shapes out of linear, blocky polygons.

Ending Geometry

This was with 270° of clean floor, still a 36' bin and a 20.4° angle of repose.

	SketchUp	Calculator
Tetrahedron	196	196
Circle Segment	30	32
Total	452 ft3	456 ft3

This time the calculator shows 4 ft³ (3 bushels) more than the SketchUp model. Still under 1% off, which is impressive given that I could see the circle segments getting more imprecise in SketchUp as the arc degrees decrease, given that a "circle" in SketchUp is actually a 24-gon which makes this 45° arc a trapezoid.

✅ So we know that the calculations that are happening in JavaScript are matching what is seen in the SketchUp model.

Real World

Since making this I've used it once and can say it's not way off. The calculator said about 850 bushels remained, and this all fit in a ~1000 bushel truck with some room to top off from another commingled bin.

As I have elevator tickets for bin finishings I will track the exact accuracy of this. If you use this calculator and have calculated vs actual numbers, please send them to me so I can adjust the formula if needed.

Each winter brings with it another seed buying decision and thus another opportunity to make some spreadsheets to overanalyze said decision. I continue to look for better ways to compare profitability between differing yield/price seed brands, so I made this simple matrix spreadsheet as a quick reference guide for breakeven yields on differing seed prices.

These breakeven bushel calculations are pretty straightforward to do, but it always feels annoying to have it as a one-off calculation for a specific pair of seeds and takes some time to do in the moment. The idea of this matrix is to be a quick lookup you can do on any two prices in the middle of a seed discussion.

The input fields are highlighted in yellow. You specify:

• Market price of the commodity
• How many dollars each row/column should be spaced
• Price (per bag) to set low end of horizontal axis
  • In the example above, cell B8 points to the value of cell M7, so an adjustment to the $160 starting price will also flow over to the vertical axis.
• Seeding population for each axis

The resulting numbers in the matrix represent how many bushels/acre it would take for the seed price on the left to be more profitable than the seed price on the top.

Alternate Configuration

The above example is good for huge variances in price (like between the $200 and $300 area) but it assumes both prices won’t be above or below $260.

For smaller variations that don’t safely reside on one side or the other of a middle price, consider setting cell M8 equal to C7. This will give you a symmetrical matrix with less range coverage, but more flexibility.

In this mode it will be less obvious which axis is the comparison variety, but you can look to the extreme corners in the upper right or bottom left to get your bearings if you forget the format.

Download

Here’s a link to a copy of this in Google Sheets. I’ve primarily used this for corn, but the spreadsheet also includes a soybean tab which uses a 140K seeds / unit calculation instead of 80K.